Consider the following problem. I have a 4-item measure of a psychological construct. Let’s call it Extraversion. Here are the four items:
- I like to go to parties
- I am a talkative person
- I see myself as a good leader
- I like to take charge
It might be obvious to some, but the first two items and the last two items are more related to each other than the other combinations of items. In fact, we could say the first two items measure the “Sociability” aspect of Extraversion while the last two items measure the “Assertiveness” aspect of Extraversion.
Now let’s say I am in a real bind because, although I love my 4-item measure of Extraversion, in my next study I only have time for a 2-item measure. Which two items should I choose?
Let’s further say that I have collected a lot of data using our 4-item measure and know that the correlation matrix among the items looks like this:
| Item 1 | Item 2 | Item 3 | Item 4 | |
| Item 1 | 1.00 | .80 | .30 | .30 |
| Item 2 | 1.00 | .30 | .30 | |
| Item 3 | 1.00 | .80 | ||
| Item 4 | 1.00 |
So as noted above, the first two items and the last two items are highly correlated, but all items are at least moderately associated. So which two items should I choose?
The Case for High Internal Consistency
At some point, almost every psychology student is taught that reliability limits validity. That is, on average, the correlation between two constructs cannot exceed the square root of the product of their reliabilities. Or more simply, scales with higher reliability can achieve higher validity. The most frequently used method of estimating reliability is undoubtedly Cronbach’s alpha. Cronbach’s alpha is a measure of the internal consistency of a scale (assuming a single factor underlies the scale). Cronbach’s alpha is also an estimate of reliability under the special condition that the items making up the scale can be thought of as a random subset of the population of items that could make up the scale. With this in mind, the obvious choices are to go with either Items 1 and 2 or Items 3 and 4. Either of those combinations will certainly have higher internal consistency in our new study.
The Case for Content Coverage
However, if we select one of the high internal consistency options, we are sacrificing content coverage in our measure. Indeed, one could easily argue that our shorter measure is now either a measure of Sociability or Assertiveness, but not Extraversion. From a logical standpoint, if we want to cover our entire construct, we should choose those items that are the least correlated with each other (in this case that any of the following combinations: 1_3, 1_4, 2_3, or 2_4). Unfortunately, all of these choices are going to have lower internal consistencies. And as noted above, a low reliability will limit our validity. Or will it?
I’ve created an example in R to work through this hypothetical, but relatively realistic, problem. Let’s first begin by creating our population correlation matrix. We will then use that population correlation matrix to generate some random data to test out our different options. Of course, because we want to examine validity, we need some sort of criterion. So to our matrix from above, I’ve added a fifth variable – let’s call it popularity – and I’m assuming this variable correlates r = .10 with each of our items (i.e., has some small degree of validity).
library(mvtnorm) mat <- matrix(c(1,.8,.3,.3,.1, .8,1,.3,.3,.1, .3,.3,1,.8,.1, .3,.3,.8,1,.1, .1,.1,.1,.1,1), ncol=5, byrow=T) set.seed(12345) # See we can get the same results dat <- rmvnorm(n=10000, sigma=mat) cor(dat[,1:4]) # Our sample correlation matrix for our key items [,1] [,2] [,3] [,4] [1,] 1.0 0.8 0.3 0.3 [2,] 0.8 1.0 0.3 0.3 [3,] 0.3 0.3 1.0 0.8 [4,] 0.3 0.3 0.8 1.0
As noted above, there are six possible combinations of items to form composites we could choose from: 1_2, 1_3, 1_4, 2_3, 2_4, and 3_4. One thing that might tip our decision about which to use is to first determine which combination of items correlates most closely with the scores we would get from our 4-item measure. The partwhole() function in the {multicon} package does this for us rapidly:
library(multicon) partwhole(dat[,1:4], nitems=2)
The argument nitems=2 tells the function that we want to look at all of the possible 2-item combinations. The results look like this (note I’ve rounded them here):
1_2 1_3 1_4 2_3 2_4 3_4 Umatch 0.82 0.96 0.96 0.96 0.96 0.82 Fmatch 0.81 0.96 0.96 0.96 0.96 0.82
The top row (1_2, 1_3, etc.) identifies the combination of items that was used to form a composite. The next row (Umatch) are the partwhole correlations between the scores for that two-item composite, using unit weighting, and the total scores yielded by averaging all four items. The third row (Fmatch) contains the partwhole correlations between the scores for that two-item composite, using component scores, and the total scores yielded from a single principle component of all four items. The numbers are very similar across rows, but in this case we care more about Umatch because we intend on creating a unit-weighted composite with our new measure.
What should be obvious from this pattern of results is that the four combinations of items that select one item from each aspect (Sociability and Assertiveness) have much stronger partwhole correlations than either of the other two (more internally consistent) combinations.
What about internal consistency? We can get the internal consistency (alpha) for our four-item measure and for each possible combination of two items measures:
alpha.cov(cor(dat[,1:4])) # For various combinations of 2 items alpha.cov(cor(dat[,1:2])) alpha.cov(cor(dat[,c(1,3)])) alpha.cov(cor(dat[,c(1,4)])) alpha.cov(cor(dat[,2:3])) alpha.cov(cor(dat[,c(2,4)])) alpha.cov(cor(dat[,3:4]))
The internal consistencies are .78 for the 4-item measure, .89 for the two Sociability items and .88 for the two Assertiveness items. Those are fairly high and fall into what many psychologists might call the “acceptable” range for reliability. The other four combinations do not fare so well with reliabilities of .46. Many people would consider these “unacceptably low.” So clearly, combinations 1_2 and 3_4 are the winners from an internal consistency standpoint.
But what about validity? Arguably, the entire point of the scientific enterprise is validity. Indeed, some might argue that the whole point of measurement is prediction. So how do our six combinations of 2-item scales do in terms of predicting our criterion?
We can use the scoreTest() function, available in the {multicon} package[1], to create our six composite scores.
myKeys <- list(OneTwo = c(1,2), OneThree = c(1,3), OneFour = c(1,4), TwoThree = c(2,3), TwoFour = c(2,4), ThreeFour = c(3,4)) out <- scoreTest(data.frame(dat), myKeys, rel=TRUE) out$rel # The same alphas as before with more information describe(out$scores)
Note that scoreTest() has an option for calculating the alphas (and other metrics of internal consistency). You can check those for consistency with the above.
Now let’s correlate our six composites with the criterion. But beyond these validity coefficients, we might also want to look at the validities if we correct for attenuation. We can do the latter by simply dividing the observed correlations by the square root of their estimated reliabilities (internal consistencies).
ObsCors <- cor(out$scores, dat[,5])
DisCors <- ObsCors / sqrt(out$rel[,1])
# Which combination is best as predicting the criterion?
round(data.frame("r"=ObsCors, "rho"=DisCors),2)
r rho
OneTwo 0.10 0.11
OneThree 0.12 0.18
OneFour 0.13 0.19
TwoThree 0.12 0.17
TwoFour 0.12 0.18
ThreeFour 0.11 0.11
So how do our results look? First in terms of observed correlations (r), the constructs that used one item from Sociability and Assertiveness outperform the constructs that use only Sociability or Assertiveness items. The picture is even clearer when we look at the corrected correlations (rho). By virtue of their high internal consistencies, neither the pure Sociability nor the pure Assertiveness composites gain much when corrected for unreliability.
So it seems, in regards to our hypothetical case here, we should prefer any combination of items that uses one Sociability and one Assertiveness item when creating our new 2-item measure of Extraversion. This might seem counterintuitive to some. To others, this might seem obvious. And actually, Guilford (1954) showed this a long time ago in his equation 14.37:
In this equation, rcomposite is the validity of a composite of N items, rxy is the average validity of each item in the composite, and rxx is the average inter-correlation of the items forming the composite. The simple R script below applies Guilford’s equation to our situation.
# Applying Guilford's Equation
AvgItemValidities <- rep(.1, 6)
NItems <- 2
AvgItemCors <- c(.8,.3,.3,.3,.3,.8)
guilford <- function(rXY, N, rXX) {
return(rXY * sqrt(N) * 1 / sqrt(1 + (N - 1)*rXX))
}
round(guilford(AvgItemValidities, NItems, AvgItemCors),3)
[1] 0.105 0.124 0.124 0.124 0.124 0.105
And the results are almost dead-on with what our simulation shows. That is, holding the number of items and the average validity of the items constant, increased internal consistency decreases composite validity. I’m not sure how many people know this. And amongst those who do, it is not clear to me how many people appreciate this fact.
Finally, to those who think this seems obvious, let me throw one more wrinkle at you. In measurement contexts (i.e., scale development) confirmatory factor analysis (CFA) is a common practice. Many people, especially reviewers, hold CFA fit results in high esteem. That is, if the model shows poor fit, it is invalid. Now, with a two-item measure, we cannot conduct a CFA because we do not have enough degrees of freedom. However, if we conduct “mental CFAs” for each of our six possible composite measures, it is obvious that model 1_2 and model 3_4 will show much better fits (i.e., they will have smaller residuals) than any of the other models. We could actually demonstrate this if we extended our example to six items and attempted to make a shorter 3-item measure. Thus, I suspect that even though much of what I said above might seem obvious to some, I also suspect that many would miss the fact that a poor CFA fit does not necessarily mean that the construct(s) being measured have poor validity. In fact, it is very possible that constructs formed from better fitting CFAs have worse predictive validity than constructs from worse fitting CFAs.
[1] This function is only available in version >=1.5 of the{multicon} package released after 1/8/2015. If you have an older version, you may need to update.
Reference
Guilford, J. P. (1954). Psychometric Methods (2nd ed.). New York: McGraw-Hill.
Note: I am grateful to Tal Yarkoni for his feedback on a prior draft of this post.

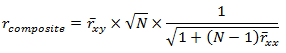
You also have to remember that the fit of a model only tells you whether the observed variances and covariances can be reproduced with reasonable accuracy by your model. This question is largely independent of the size of the correlations/covariances among manifest variables (i.e., items in your case). So you can get a perfectly fitting model when the correlations among items are effectively zero or when they are very high. Further, good fit tells you very little about whether you have the correct model. There are many many models that you can fit to any set of manifest variables and quite a few of these may exhibit “good” fit. Even causally misspecified models can give you great fit.